(스터디 내용 정리) step05. 역전파 이론

less than 1 minute read

지난 step에서 수치 미분(numerical differentiation)으로 미분 연산을 수행했다. 이번 step에서는 역전파의 개념을 서술한다.

1. 연쇄 법칙(chain rule)

많은 함수는 합성 함수이다. 특히 딥러닝에서 쓰이는 심층 신경망의 경우, 각 층에서 입력과 출력이 존재하여 그 사이 관계가 함수로 나타난다.

예를 들어 다음과 같은 함수가 있다고 가정하자.

$y=F(x)$ $F(x)=C(B(A(x)))$

도식화하면 다음과 같다. 이를 미분한다면 다음과 같다.

${dy\over dx} = {dy\over dv}{dv\over du}{du\over dx}$

이 책에서는 앞에 1을 추가해서 연산한다.

${dy\over dx} = {dy\over dy}{dy\over dv}{dv\over du}{du\over dx}$

곱셈 순서를 바꿔도 결과는 같다.

만약 다음과 같은 순서로 계산한다면,

${dy\over dx} = (({dy\over dy}{dy\over dv}){dv\over du}){du\over dx}$

$F’(x)=C’(v)B’(u)A’(x)$

와 같은 셈이다.

이를 그림으로 비교한다면 다음과 같이 표현할 수 있다.

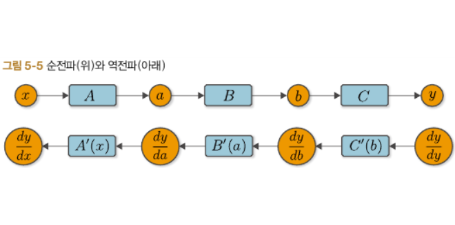
곱의 순서를 바꾸면 미분 연산이 출력에서 입력으로 거슬러 올라가는 것처럼 보인다.